| Y1 |
| · · · |
| Ym |
| Y1 | ... | Ym |
Dans l'exemple de la formule (¬ AÙ C)Ú A Ú (BÙ (¬ CÚ D)) ci-dessus, les chemins verticaux complètement expansés (ceux qui ne contiennent que des littéraux) sont {¬ A, A, B}, {¬ A, A, ¬ C, D}, {C, A, B}, {C, A, ¬ C, D}.
La notion de chemin vertical est tout à fait similaire à celle des chemins dans les tableaux. En fait, on peut transformer tout chemin atomique de tableau en un chemin vertical complètement expansé à condition de convertir les formules +A en A et -A en ¬ A. Et réciproquement, tout chemin vertical complètement expansé peut être transformé en en chemin atomique de tableau en traduisant A en +A et ¬ A en -A.
La méthode des connexions procède ensuite comme la méthode des tableaux de la section 1 : nous expansons les chemins verticaux et essayons de les clore tous ensemble par unification; et pour représenter les étapes d'extension, nous ajoutons des versions renommées génériques de Y en bas de la matrice courante tout entière, ce qui a pour effet d'étendre tous les chemins verticaux automatiquement.
Une paire complémentaire de littéraux dans un chemin vertical est appelée une connexion par Bibel; l'analogue des tableaux, vus comme des ensembles de chemins, est appelé un pré-couplage (``pre-mating'' en anglais) par Andrews, et un ensemble couvrant de chemins (``spanning set of paths'' en anglais) par Bibel. Un ensemble couvrant de connexions est un ensemble de connexions tel que tout chemin d'un pré-couplage a une connexion dans l'ensemble. Dans la méthode des tableaux, nous cherchions à clore tous les chemins; ici nous cherchons un ensemble couvrant unifiable de connexions. À part le vocabulaire, peu de choses changent comparées à la méthode des tableaux, c'est pourquoi nous ne décrirons pas la méthode plus avant. Son principal avantage est informatique, car nous pouvons représenter les connexions comme des liens dans ce qu'on appelle un graphe de connexions, sur lequel diverses opérations combinatoires peuvent être effectués efficacement. Voir [Bib87] pour une description technique complète.
3.2 Comparaison avec la résolution
Nous allons voir qu'il existe des parallèles entre les tableaux et la résolution. La première qu'il nous faut remarquer, cependant, est que la résolution fonctionne uniquement en logique classique (au moins sans quelques modifications), de sorte que la comparaison que nous allons effectuer sera limitée à la logique classique, et en fait à la logique classique du premier ordre.La second difficulté à laquelle nous faisons face est que la résolution et les tableaux ne résolvent pas le même problème, de la façon dont nous les avons définis. Parce que nous avons tenté de présenter les deux méthodes en les dérivant de systèmes de séquents à la Gentzen, nous avons décrit la résolution comme une méthode de recherche de réfutations (sémantiquement, qui essaie de montrer qu'une formule est insatisfiable), et les tableaux comme une méthode de recherche de preuves (sémantiquement, qui essaient de montrer qu'une formule est valide). Pour les comparer, nous devons donc modifier soit la résolution pour qu'elle devienne une procédure de preuve, soit la méthode des tableaux pour en faire une procédure de réfutation.
Chacune de ces modifications est également facile, parce que F est prouvable (resp. valide) si et seulement si ¬F est incohérente (resp. insatisfiable). Mais le processus demande une certaine agilité mentale. Pour des raisons historiques, la résolution et les tableaux sont usuellement présentés comme des procédures de réfutation. Nous pensons que ce n'est pas naturel, au moins dans le cas des tableaux : les tableaux en style de recherche de réfutation nous forcent en général à raisonner en termes de modèles, autrement dit sémantiquement, alors que les tableaux peuvent aussi être utilisés pour des logiques dont la sémantique est encombrante, comme les logiques linéaire ou intuitionniste.
Pour cette raison, et pour montrer qu'en aucun cas les procédures de réfutation ne sauraient se montrer supérieures aux procédures de preuve directe (une erreur courante), nous redonnons la définition de la résolution, mais cette fois-ci en forme de recherche de validité :
Définition 4 [Résolution positive] Supposons que nous voulions prouver une formule existentielle F= $ x1· ... $ xn· Y, où Y est en forme normale disjonctive (dnf), c'est-à-dire que Y est une disjonction de clauses conjonctives.
La règle de résolution binaire positive est :
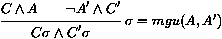
où nous supposons que les deux clauses CÙ A et ¬ A'Ù C' ont été renommées pour n'avoir aucune variable libre en commun. La conclusion de la règle est appelée le résolvant binaire des deux clauses, les prémisses sont appelées les clauses parentes, et A (resp. ¬ A') est le littéral sur lequel on résout dans la première clause (resp. la seconde clause).
Nous disons que les littéraux A et ¬ A' sont complementaires si A s'unifie avec A'.
La règle de factorisation positive est :
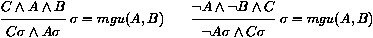
La conclusion de la règle est appelée un facteur binaire de la clause prémisse.
Un facteur d'une clause est soit la clause elle-même, soit un facteur binaire d'un de ses facteurs. Un facteur propre d'une clause est un facteur d'un de ses facteurs binaires.
Un résolvant de deux clauses est un résolvant binaire de facteurs de chaque clause, non nécessairement propres.
Une dérivation par résolution positive est un arbre inversé dont les noeuds sont étiquetés par des clauses, les feuilles sont étiquetées par des clauses de l'ensemble initial de clauses, et les noeuds internes ont comme prédécesseurs leurs clauses parentes.
Une preuve par résolution positive est une dérivation se terminant sur la clause vide, autrement dit une dérivation dont la racine est étiquetée par la conjonction vide T (valant le vrai).
Tout le chapitre sur la résolution se traduit au cas de la résolution positive. Ici, ce ne sont pas les résolvants qui sont impliqués par leurs clauses parentes, mais le contraire : les résolvants impliquent la disjonction de leur clauses parentes (conjonctives); si nous dérivons T, la disjonction des clauses ancêtres de T qui sont dans l'ensemble de clauses de départ est valide, ce qui prouve l'ensemble de clauses de départ. Aussi, pour prouver un énoncé F modulo un ensemble d'axiomes A, le fait de mettre AÞF en dnf revient à mettre ¬A et F en dnf; c'est ce qui correspond à la conversion de A et ¬F en cnf, en résolution usuelle (qui est une méthode de réfutation). Finalement, tous les raffinements de la résolution se transposent quasiment sans modification.
Ce qui correspond aux clauses conjonctives de la résolution positive dans les tableaux (ou la méthode des connexions) est la notion de chemins orthogonale à celle que nous avons utilisée en section 3.1 :
Définition 5 [Chemins] Soit Y une formule sans quantificateur en nnf, représentée sous forme matricielle.
L'ensemble des chemins horizontaux dans Y est le plus petit ensemble tel que :
- {Y} est un chemin horizontal;
- si C est un chemin horizontal contenant une formule Y'
de la forme :
alors C\ {Y'}È {Y1, ..., Ym} est un chemin horizontal;Y1 ... Ym - si C est un chemin horizontal contenant une formule Y' de la forme :
alors C\ {Y'}È {Yi}, 1£ i£ m, sont des chemins horizontaux.Y1 ·
·
·Ym
Par exemple, les chemins horizontaux complètement expansés de notre exemple (¬ AÙ C)Ú A Ú (BÙ (¬ CÚ D)) sont {¬ A, C}, {A}, {B,¬ C}, {B,D}. Autrement dit, une dnf de la formule est l'ensemble de clauses conjonctives suivant :
¬ AÙ C A BÙ¬ C BÙ D
En bref, alors que les tableaux essaient de clore des chemins verticaux, la résolution (positive) combine des paires de chemins horizontaux. De plus, la résolution intègre automatiquement les étapes d'extension des tableaux en ajoutant systématiquement les résolvants comme de nouvelles clauses renommées à l'ensemble courant des clauses. D'un autre côté, la résolution fonctionne en représentant explicitement toutes les clauses, alors qu'elles restent implicites dans les tableaux. (But on peut facilement adapter la résolution pour qu'elle fonctionne sur l'ensemble des chemins horizontaux d'une formule sans la convertir explicitement en clauses : c'est la résolution non clausale.)
Dans les deux sections qui suivent, nous verrons deux façons d'établir un lien entre la résolution et les tableaux. La première adapte la résolution pour fonctionner comme les tableaux, en dissociant les étapes d'extension des étapes de clôture des chemins. La second adapte les techniques de tableaux à la forme de clauses conjonctives, et fournit ce qui s'appelle la technique d'élimination des modèles.
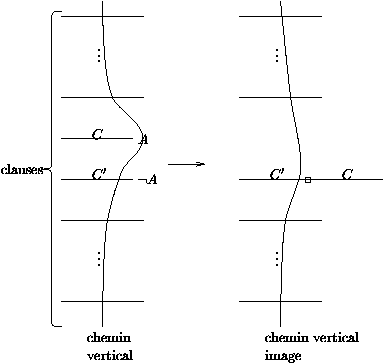
Figure 5: Effet du calcul des résolvants sur les chemins verticaux3.3 La V-résolution de Chang
Quand nous créons de nouveaux résolvants par la règle de résolution, nous renommons toutes ses variables libres, de sorte que deux clauses n'aient jamais de variables libres en commun. Implicitement, les clauses C sont quantifiées existentiellement en résolution positive (elles abrègent $ x1· ... $ xn· C), de sorte que la génération d'une instance de la clause avec de nouvelles variables revient exactement au même que l'utilisation d'une g-règle.
L'idée de Chin-Lian Chang [CL73] est alors de limiter cet effect en ne renommant pas les variables libres des nouvelles clauses. Pour montrer qu'un ensemble S de clauses conjonctives est valide, nous produisons à l'avance un nombre fixé k(C) de versions renommées Cr1, ..., Crk(C) de chaque clause C de sorte qu'aucune paire de clauses n'ait de variable libre en commun, ce qui fournit un nouvel ensemble S' de clauses conjonctives. Nous cherchons ensuite une substitution s telle que S's soit propositionnellement valide, en appliquant la règle de résolution propositionnelle, relevée au cas sans quantificateur comme suit. Associons à chaque clause une substitution, initialement vide. Nous appliquons ensuite les règles suivantes de V-résolution:
- Factorisation : étant donnée une clause CÙ AÙ B associée à la substitution s, où A et B sont des atomes, q est le mgu de A et B et s' est le mgu de q et s, remplacer CÙ AÙ B par CqÙ Aq; (et de même pour les clauses CÙ¬ AÙ¬ B;)
- Résolution binaire : étant données deux clauses CÙ A (de substitution associée s) et ¬ A'Ù C' (de substitution associée s'), où q est le mgu de A et A', q' est le mgu of s et s', et s'' est le mgu de q et q', produire la clause conjonctive CqÙ C'q, de substitution associée s''.
La factorisation et la résolution binaire doivent être appliquées de façon non déterministe, exactement comme dans le cas des règles d'expansion des tableaux. Pour comparer les deux méthodes, regardons l'effet de la V-résolution sur les chemins verticaux.
Soit S0 un ensemble de clauses conjonctives. Choisissons un atome A1 apparaissant dans S0, et calculons l'ensemble S1 de tous les résolvants de clauses dans S0 sur A1 et ¬ A1. S1 est alors logiquement équivalent à " A1· S0. (De façon opposée, dans le cas de la réfutation, nous avons vu que le calcul de tous les résolvants sur un atome revenait à calculer $ A1· S0, et qu'il s'agissait de la règle de séparation de Davis-Putnam.) Regardons maintenant de quelle façon les chemins verticaux complètement expansés dans S0 se retrouvent transformés dans S1. Consulter la figure 5 pour une illustration de ce qui arrive, au cas où le chemin vertical considéré passe par A mais pas par ¬ A. En général, étant donné un chemin vertical P dans S0 qui ne contient pas à la fois A et ¬ A, nous trouverons un ou plusieurs chemins dans S0 dans lesquels P\ {A,¬ A} est inclus. D'un autre côté, si P contient à la fois A et ¬ A, alors il ne correspondra à aucun chemin vertical dans S1. (Sur la figure, un tel chemin à droite devrait rencontrer la clause résolvante C'Ù C à un endroit --- un littéral --- ou il rencontrait déjà C ou C' sur le côté gauche de la figure, mais un tel chemin n'existe pas.) Autrement dit, le calcul de l'ensemble de tous les résolvants sur un atome A clôt tous les chemins verticaux que l'on peut clore sur A et ¬ A, tout en augmentant en général le nombre de chemins restant à clore. (Mais n'oublions pas que, comme les chemins restent implicites, ils sont automatiquement partagés : nous n'avons jamais deux copies du même chemin.)
La V-résolution n'est pas particulièrement intéressante en pratique. En effet, elle combine les pires aspects des tableaux (le non-déterminisme de la recherche, où des chemins différents peuvent être redondants mais seront cependant explorés de façon totalement indépendante) et les pires aspects de la résolution (l'utilisation de la résolution propositionnelle comme processus de base de recherche de preuve propositionnelle). Elle est cependant intéressante comme exemple des connexions qui peuvent exister entre les tableaux et la résolution.
3.4 Élimination de modèles
Une interaction beaucoup plus intéressante entre les tableaux et la résolution est la procédure d'élimination de modèles de Donald Loveland, aussi connue sous le nom d'OL-resolution, une forme de résolution linéaire sur des clauses ordonnées. D'autre part, nous pouvons la voir comme une variante de la méthode des tableaux de base, qui travaille sur des formules en nnf.
Supposons que nous voulions prouver un ensemble de clauses conjonctives S, contenant une clause but distinguée L1Ù ...Ù Lk. Soit S' l'ensemble S moins cette clause but. Soit T un tableau, autrement dit un ensemble de chemins. Initialement, T consiste uniquement en les chemins unitaires {L1}, ..., {Lk}. Soit aussi s une substitution, initialement vide. L'élimination de modèles fonctionne par transformation du tableau et de la substitution en utilisant des clauses de S' pour étendre les chemins du tableau T, par les deux règles suivantes :
- Extension : prendre un chemin P de T, et un littéral A
(resp. ¬ A) de P; choisir de façon non déterministe
une clause conjonctive ¬ A'Ù L1Ù ... Ln
(resp. A'Ù L1Ù ...Ù Ln) dans S' (dont
les variables libres ont été renommées en de nouvelles
variables) telle que As et A's soient unifiables.
Ensuite, soit s' le mgu obtenu, remplacer s par
ss', et remplacer P par les chemins PÈ
{Li}, 1£ i£ n dans T. En bref :
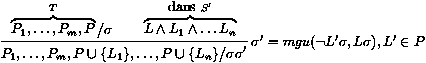
- Réduction : prendre un chemin P de T, et un littéral A
(resp. ¬ A) de P; choisir de façon non déterministe un
littéral ¬ A' (resp. A') dans P tel que As et
A's soient unifiables. Ensuite, soit s' le mgu
obtenu, remplacer s par ss', et effacer P de
T. En bref :
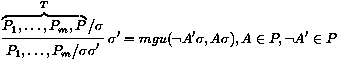
L'élimination de modèles est une procédure de preuve correcte et complète, mais nous ne le montrerons pas. À la place, nous allons montrer les relations entre l'élimination de modèles, les tableaux et la résolution linéaire. Nous invitons le lecteur à adapter les preuves de correction et de complétude des tableaux ou de la résolution linéaire à l'élimination de modèles après avoir lu les sous-sections qui suivent.
3.4.1 L'élimination de modèles, une méthode de tableaux
Nous pouvons interpréter ces règles comme des règles de tableaux. L'extension consiste à effectuer une g-expansion sur une clause de S', suivie d'une a-expansion sur le connecteur n-aire conjonctif Ù. La b-expansion est traitée automatiquement par le fait de prendre la clause à l'intérieur de l'ensemble S' : bien que les autres clauses n'apparaissent pas sur le chemin P, elles n'en ont pas besoin, car nous ne nous intéressons qu'aux chemins consistant en des littéraux. Plus exactement, comme nous fermons les chemins en n'unifiant que des formules signées atomiques, la seule partie qui nous intéresse dans les chemins est l'ensemble des formules atomiques signées qui s'y trouvent.
D'autre part, les étapes de réduction sont l'analogue de la règle de clôture des tableaux. Mais tous les chemins ne sont pas clos par des étapes de réduction, puisque l'extension d'un chemin par une clause unitaire (m=0) a aussi pour effet de le clore.
Les contraintes que l'élimination de modèles impose au processus d'expansion des tableaux sont les suivantes. D'abord, nous devons deviner une clause but; ceci veut dire que nous devons initialiser l'expansion du tableau en b-expansant l'ensemble S des clauses, et en choisissant une des clauses à a-expanser. Ensuite, toutes les autres expansions sont fortement contraintes : nous exigeons que, chaque fois que nous expansons une clause, au moins un des cheminus obtenus est immédiatement clos. (Il s'agit de la condition d'unification de la règle d'extension.) Finalement, comme en résolution, toute a-expansion d'une clause est précédée par une g-expansion systématique, autrement dit par une renommage de ses variables libres.
Pour illustrer le processus, considérer l'ensemble de clauses :
AÙ B AÙ ¬ B ¬ AÙ B ¬ AÙ¬ B
Choisissons par exemple AÙ B comme clause but. Le tableau initial est alors :
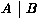
Étendons le chemin de gauche en utilisant par exemple la clause ¬ AÙ B, ce qui donne :
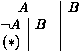
où l'extension sur A vient de clore le chemin le plus à gauche. Nous représentons cela par le signe *. Nous continuons par exemple en étendant le chemin non clos le plus à gauche par ¬ AÙ ¬ B, ce qui donne :
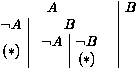
Mais maintenant, nous pouvons clore le chemin non clos le plus à gauche {A,B,¬ A} par la règle de réduction. Si nous continuons, nous aboutirons au tableau qui suit, où tous les chemins sont clos, soit par extension (ce qui est signalé par une astérisque *) soit par réduction (ce qui est signalé par un petit cercle °) :
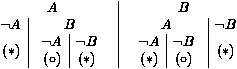
Bien que l'exemple soit propositionnel, le cas du premier ordre n'est compliqué que par le besoin de maintenir une substitution qui s'applique au tableau tout entier, et qui est calculée par unification.
3.4.2 L'élimination de modèles, une résolution linéaire
Nous pouvons aussi interpréter ces règles comme des règles de résolution linéaire. En effet, un tableau T peut être vu comme une représentation spéciale de la clause courante au sommet : il suffit de lire les littéraux qui restent en bas des chemins non clos du tableau. Par exemple, le premier tableau ci-dessus représente la clause AÙ B (le tableau initial, de toute façon, doit représenter la clause but), le deuxième représente la clause BÙ B (avant contraction), et le dernier représente la clause vide.
Alors l'application de la règle d'extension revient à calculer un résolvant binaire entre la clause courante au sommet en tant que clause centrale et une clause d'entrée (une clause de S') en tant que clause latérale : les extensions sont des étapes d'input-résolution.
En fait, la structure de tableau est plus riche que la simple description de la clause courante au sommet. Nous pouvons en effet extraire les tableaux qui avaient été produits avant le tableau courant, sous forme de sous-tableaux du tableau courant. (Un tableau étant un arbre, nous considérons comme sous-tableau n'importe quel sous-arbre du tableau courant.) Alors, au moins dans le cas propositionnel, la règle de réduction peut être vue comme une étape de résolution entre la clause centrale et une clause ancêtre, c'est-à-dire une clause qui n'est pas une clause d'entrée, qui est restée codée sous forme d'un sous-tableau du tableau courant.
Faisons-en la démonstration sur l'exemple ci-dessus. Le premier tableau correspond à la clause but AÙ B. Ensuite, le deuxième tableau correspond à la clause BÙ B, mais le B de gauche peut être remplacé par son littéral parent A, et ainsi nous retrouvons la clause de départ AÙ B. Le troisième tableau représente ¬ AÙ B, mais aussi les clauses précédentes BÙ B et AÙ B. Ensuite, si nous appliquons la règle de réduction sur A et ¬ A, nous résolvons la clause au sommet ¬ AÙ B avec la clause ancêtre AÙ B. Ceci produit B, qui est exactement le résultat que nous lisons en bas du troisième tableau, une fois que nous avons clos le chemin de gauche par une règle de réduction.
Au premier ordre, la règle de réduction fait quelque chose de légèrement différent en réalité que la résolution binaire avec une clause ancêtre, parce que l'ensemble des variables libres dans le tableau courant est laissé intact. Autrement dit la règle de réduction calcule un résolvant binaire sans renommage de la clause centrale ou de la clause ancêtre. De façon étonnante, non seulement ceci ne met pas en danger la complétude de la procédure, mais en fait cela nous permet de nous passer complètement de la règle de factorisation !
Considérons l'exemple traditionnel où nous avions besoin de la factorisation :
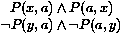
La résolution était incomplète sans la factorisation sur cet exemple, parce que le seul résolvant binaire que nous pouvions produire était P(a,a)Ù ¬ P(a,a). En élimination de modèles, le fait de choisir la première clause comme but par exemple nous mène au tableau initial suivant :
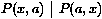
Ensuite nous étendons le chemin de gauche par une nouvelle version renommée de la seconde clause, ce qui donne :
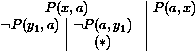
avec comme substitution [a/x,a/y1]. Appliquons la règle de réduction sur le chemin non clos de gauche, puis étendons le chemin de droite par une version renommée de la deuxième clause de nouveau, et réduisons finalement le chemin de droite. Nous obtenons :
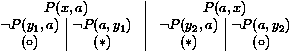
avec comme substitution [a/x,a/y1,a/y2]. Nous n'avons pas eu besoin de factoriser aucune clause, parce que la variable x que nous lions dans la moitié gauche du tableau et la variable x que nous lions dans la moitié droite sont les mêmes, ce qui a donc pour effet d'instancier la première clause en P(a,a), c'est-à-dire en la clause que nous ne pouvions obtenir que par factorisation de la première clause en résolution classique.
- Historiquement, l'élimination de modèles a été inventée dans les années 1970 par Donald Loveland comme un raffinement particulier de la résolution, et diverses formes de résolution linéaire on été développées par Robert Kowalski. Cette procédure a été appelée ``élimination de modèles'' après que l'on a découvert que ce que la méthode faisait, essentiellement, était d'énumérer des (ensembles d') interprétations sous forme de chemins dans le tableau, et d'ensuite montrer qu'elles n'étaient pas des modèles de la formule but en fermant le chemin. En fait, c'est une façon générale de comprendre les tableaux en tant que méthodes de réfutation. Par dualité, les chemins dans les tableaux réfutationnels sont à voir comme des conjonctions, de sorte que les chemins complètement expansés sont des conjonctions de littéraux. Les instances de tels chemins qui ne contiennent pas à la fois un atome et sa négation sont des interprétations de Herbrand partielles. Pour réfuter le but, nous devons trouver des isntances telles qu'aucun chemin ne peut être vu comme une interprétation partielle de Herbrand, autrement dit nous fermons tous les chemins.



- si C est un chemin horizontal contenant une formule Y' de la forme :