Tableaux au premier ordre

1 Tableaux au premier ordre

Grâce au théorème d'élimination des coupures pour la logique du premier ordre, nous pouvons restreindre l'espace de recherche des preuves d'un séquent donné G ¾® D à celui des preuves sans coupure. C'est exactement ce que nous avons fait dans le cas des tableaux propositionnels.

Dans cette section, nous examinons les façons de chercher une preuve d'une formule existentielle F. Pour prouver une formule arbitraire du premier ordre, nous pouvons toujours commencer par l'herbrandiser pour en faire une formule existentielle, ce qui signifie que nous ne perdons pas en généralité en faisant cela. Nous traiterons des formules générales du premier ordre directement en section 2.

On peut rechercher une preuve sans coupure dans LK de F = $ x₁ · ... $ x_n · Y, où Y est sans quantificateur, essentiellement de la même façon qu'avec les tableaux propositionnels. La seule différence est que nous devons traiter de la règle supplémentaire $R. Ceci pose un nouveau problème : pour prouver G ¾® D, $ x·F en utilisant $ x·F comme formule principale, nous devons deviner une instance F[t/x] de F, et produire G ¾® D, $ x·F, F[t/x], ou bien G ¾® D, F[t/x].

Comme l'affaiblissement à droite des séquents est admissible dans le système classique LK, si G ¾® D, F[t/x] est prouvable, alors G ¾® D, $ x·F, F[t/x] aussi. Donc il suffit de chercher des preuves de cette dernière. Mais, comme $ x· F reste présent sur le côté droit, le processus peut se répéter à l'infini : la recherche de preuve peut ne pas terminer. Mais nous devons conserver de telles duplications pour rester complet. Ce que nous avons fait là, logiquement, c'est d'appliquer $R couplé avec une instance de la règle de contraction. La logique linéaire résout le problème. La logique intuitionniste le résout aussi, en interdisant purement et simplement les affaiblissements à droite. Mais dans ces logiques, la recherche de preuve est en fait considérablement plus difficile qu'en logique classique; notamment, on ne peut déjà pas convertir les formules en forme prénexe.

1.1 Utilisation du théorème de Herbrand

La solution la plus simple est d'utiliser le théorème de Herbrand : F est prouvable si et seulement s'il existe un entier k, et k substitutions s₁, ..., s_k telles que ¾® Ys₁, ..., Ys_k soit dérivable dans LK. Comme on peut éliminer les coupures des preuves de LK, et comme les preuves sans coupure ont la propriété de sous-formule, cette dernière condition est équivalente à : ¾® Ys₁, ..., Ys_k est dérivable en LK₀ sans coupure.

Nous pouvons donc étendre la méthode des tableaux propositionnelle au premier ordre comme suit :

Deviner un entier k;
Deviner k substitutions s₁, ..., s_k;
Appliquer la méthode des tableaux propositionnelle pour déterminer s'il existe une preuve sans coupure de ¾® Ys₁, ..., Ys_k.

Cette procédure naïve demande un travail énorme de divination. Mais on peut remplacer la tâche consistant à deviner les substitutions s_i par le calcul d'unificateurs, comme c'était déjà le cas pour la résolution.

En premier, au lieu de deviner k substitutions, on peut se ramener à n'en deviner qu'une. Soient Y₁, Y₂, ..., des versions renommées de la formule Y, et d'ensembles de variables libres deux à deux disjoints. Nous devons trouver k substitutions telles que ¾® Y₁s₁, ..., Y_ks_k soit prouvable, ou de façon équivalente juste une substitution s telle que (¾® Y₁, ..., Y_k)s soit prouvable : s égale s₁ È ... È s_k, et réciproquement, s_i est s restreinte à fv(Y_i), 1£ i£ k.

(a-règles) (b-règles)

a a₁ a₂

+(XÙ Y) +X +Y

-(XÚ Y) -X -Y

-(XÞ Y) +X -Y

+(¬ X) -X

-(¬ X) +X

b b₁ b₂

-(XÙ Y) -X -Y

+(XÚ Y) +X +Y

+(XÞ Y) -X +Y

Figure 1: Règles de tableaux

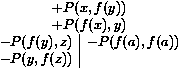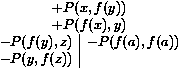
Ainsi, il suffit de trouver une substitution s qui instancie le séquent donné G ¾® D en un que nous pouvons démontrer en LK₀ sans coupure. Au lieu de deviner s, nous le calculons en nous laissant guider par l'expansion du tableau. Remarquons que les a-règles et les b-règles (voir figure 1) sont inchangées par notre connaissance ou notre ignorance de la substitution à appliquer aux formules sur le chemin courant. Le seul changement est dans la façon de clore des chemins, c'est-à-dire dans la façon d'utiliser la règle Ax : au lieu de clore un chemin G ¾® D en trouvant une formule qui soit à la fois dans G et D, nous devons trouver une formule F₁ dans G et une formule F₂ dans D telles que F₁s = F₂s pour une certaine substitution s. Lorsque F₁ et F₂ sont des formules atomiques, c'est simplement le problème de l'unification. Nous devons ensuite appliquer la substitution s que nous avons trouvée au reste de la preuve en cours de construction avant de continuer à clore d'autres chemins. Expliquons cela plus en détail.

Pour suivre la tradition d'économie de mémoire des tableaux, voici la méthode en profondeur d'abord d'expansion des tableaux, définie par une procédure non déterministe prove. prove prend deux arguments, une liste l de formules signées (le chemin courant) et la substitution courante s. prove(l,s) retourne soit une nouvelle substitution s' qui clôt tous les chemins obtenus par expansion à partir de ls, ou un symbol spécial échec, qui signifie qu'il n'existe aucune substitution vérifiant cette propriété:

Choisir de façon non déterministe entre clore la branche courante (trouver une formule atomique positive +F et une formule atomique négative -F' dans l telles que Fs et F's soient unifiables de mgu s', et retourner ss'), ou ce qui suit :
si l ne contient que des atomes signés, alors retourner échec;
sinon, appliquer la stratégie d'expansion pour choisir une formule signée non atomique F dans l, et soit l' égale l moins cette occurrence de F.
- Si F est une formule de type a (de formules filles F₁, ..., F_n), alors : si prove(F₁::l',s) retourne échec, retourner échec; sinon, soit s₂ la substitution retournée, alors si prove(F₂::l',s₂) retourne échec, retourner échec; sinon, ..., soit s_n égale prove(F_n-1::l',s_n-1), et retourner prove(F_n::l',s_n).
- si F est une formule de type b (de formules filles F₁, ..., F_n), alors retourner prove(F₁::...::F_n::l',s).

Ceci est quasiment la réalisation que nous avons donnée pour les tableaux propositionnels, sauf pour ce qui est du choix non déterministe de la première étape. Illustrons ce qu'il signifie sur un exemple. Supposons que nous voulions prouver :

$ x· $ y· $ z·

(P(f(y),z)Ù P(y,f(z)))Ú P(f(a),f(a))

Þ P(x,f(y))Ú P(f(x),y)

Par le théorème de Herbrand, et en devinant le nombre 1 comme nombre d'instances nécessaires k, nous devons expanser et clore le tableau à partir du chemin initial :

+(P(f(y),z)Ù P(y,f(z)))Ú P(f(a),f(a))

Þ P(x,f(y))Ú P(f(x),y)

Puisqu'il n'y a pas de paire complémentaire de formules atomiques, nous devons expanser la formule ci-dessus. Après quelques étapes d'expansion, nous obtenons :

Maintenant, nous pouvons décider de clore le chemin de gauche en premier par exemple, mais il y a quatre paires complémentaires possibles, correspondant à trois mgu différents :: [z/x,z/y], [f(y)/x,f(y)/z] et [z/x,f(z)/y]. Si nous choisissons [z/x,z/y], alors la substitution courante s passe de [] à [z/x,z/y], et le chemin de droite s'instancie par cette dernière substitution en {+P(z,f(z)), +P(f(z),z), -P(f(a),f(a))}, qu'on ne peut pas clore. Il faut donc rebrousser chemin et choisir un autre mgu, par exemple [f(y)/x,f(y)/z]. La substitution courante s est maintenant [f(y)/x,f(y)/z], et le chemin de droite s'instancie en {+P(f(y),f(y)), +P(f(f(y)),y), -P(f(a),f(a))}, que l'on peut clore en unifiant P(f(y),f(y)) avec P(f(a),f(a)), ce qui donne la substitution finale [f(a)/x,f(a)/z].

Parce qu'on a besoin de rebrousser chemin (``backtrack'' en anglais), Prolog est considéré comme un langage idéal pour réaliser des prouveurs de théorèmes à base de tableaux. Un prouveur à base de tableaux qui est à la fois petit et efficace (pour de petits problèmes au moins) est décrit dans [BP94]. Il s'agit cependant d'un prouveur basé sur la variante dite des tableaux à variables libres: voir la section 2.

Théorème 1 [Correction, complétude] Soit F une formule existentielle $ x₁· ... $ x_n· Y.

F est prouvable en LK si et seulement s'il existe un entier k, une substitution s, et une expansion de tableau à partir du chemin {Y₁, ..., Y_k} qui est close par s.

Plus précisément, étant donnée une stratégie d'expansion f, si F est prouvable, alors la procédure de tableaux ci-dessus termine et retourne une telle substitution s comme résultat, pour k assez grand.
Preuve : Si s clôt une expansion de tableau partant de {Y₁, ..., Y_k}, alors ¾® Y₁s, ..., Y_ks est dérivable en LK, donc F est prouvable.

Réciproquement, supposons que F soit prouvable en LK. Par le théorème de Herbrand, il existe une substitution s telle que ¾® Y₁s, ..., Y_ks soit dérivable en LK₀ sans la coupure (Cut). Donc le tableau (propositionnel) complètement expansé T obtenu à partir du chemin {+Y₁s, ..., +Y_ks} voit tous ses chemins clos. Nous relevons ceci au premier ordre en considérant la tableau complètement expansé T' partant du chemin {+Y₁, ..., +Y_k} : soit C un chemin arbitraire dans ce tableau complètement expansé, alors Cs doit aussi est un chemin complètement expansé de T', et donc il doit être clos par s. Maintenant, soient C₁, ..., C_m les chemins dans T' : pour tout i, 1£ i£ m, s unifie une paire de formules atomiques A_i et B_i de signes opposés dans C_i. Donc il existe un mgu simultané de toutes les paires A_i, B_i, 1£ i£ m, que l'on trouvera nécessairement en choisissant de façon non déterministe les paires A_i, B_i et en calculant le mgu simultané paire par paire. ¤

La preuve montre qu'il n'est en fait pas nécessaire d'effectuer un choix non déterministe entre le fait de clore le chemin courant et de l'expanser : la procédure reste complète si nous forçons l'expansion de tous les chemins qui contiennent au moins une formule non atomique, et que nous ne tentions de clore que les chemins atomiques. Ce faisant, nous réduisons le non-déterminisme, mais cela nous force à attendre que tous les chemins aient été totalement expansés avant de les clore, c'est-à-dire essentiellement à attendre d'avoir un nombre exponentiel de chemins à clore. Ainsi, le fait d'expanser avant de clore n'est pas réaliste en général, et nous préférons essayer de clore chaque chemin aussi tôt que possible, bien que cela puisse augmenter le non-déterminisme.

Nous procédons comme suit. Nous essayons d'abord d'unifier des formules atomiques de signes opposés sur le chemin courant, et de retourner l'unificateur correspondant. Si le reste de la recherche échoue, alors le prouveur rebrousse chemin et essaie le choix suivant de paire complémentaire à unifier. S'il n'en reste aucune, alors le prouveur essaie d'expanser une formule de type a ou b. Si ce n'est pas possible, le prouveur rebrousse chemin au dernier point de choix, ou échoue s'il n'y en a pas. On peut faire un peu mieux en s'arrangeant pour que le prouveur évite d'unifier des paires complémentaires dont on sait déjà qu'elles ne mènent pas à une preuve : on conserve le chemin courant sous forme d'une liste v de formules atomiques signées anciennes, n de formules atomiques signées nouvelles, et exp de formules à expanser. Lorsque nous expansons une formule de exp, nous commençons par ajouter toutes les formules de n à v, et nous réinitialisons n à la liste vide; ensuite, nous expansons la formuleet mettons les sous-formules engendrées dans exp pour celles qui ne sont pas atomiques, ou dans n sinon. Nous pouvons ensuite nous restreindre à n'essayer de fermer le chemin courant qu'en unifiant une formule de n avec une formule de signe opposé dans v.

1.2 Étapes d'extension

Étant donné k, nous sommes maintenant capables de décider si ¾® Y₁, ..., Y_k a une instance prouvable en LK₀. Comment devinons-nous k ?

La réponse est que nous ne le pouvons pas. En tous cas, nous ne pouvons pas calculer le k le plus petit dont nous aurions besoin, ou même un majorant quelconque de ce k. La raison est que la logique du premier ordre est indécidable. En effet, supposons que nous puissions calculer une valeur de k à partir de la formule existentielle F, de sorte que si F est prouvable, alors ¾® Y₁, ..., Y_k a une instance prouvable. Alors nous pourrions décider si F est prouvable en calculant un tel k, puis en appliquant l'algorithme (qui termine) décrit dans la section précédente. Ceci nous fournirait un moyen pour décider de la prouvabilité de F par machine, ce qui est impossible.

Il nous faut donc réellement deviner k. Une façon de faire est d'utiliser l'approfondissement itératif (``iterative deepening''). Initialiser k à 1, et appliquer la procédure de tableaux pour savoir si ¾® Y₁ a une instance prouvable. Si oui, alors F est prouvée. Sinon, incrémenter k et réappliquer la procédure pour savoir si ¾® Y₁, Y₂ a une instance prouvable. Si oui, alors F est prouvée. Sinon, incrémenter k, et ainsi de suite.

L'approfondissement itératif combiné avec la recherche en profondeur d'abord comme dans la section précédente, est une façon commune de coder les tableaux. Comme nous l'avons déjà dit dans le cadre de la résolution, la recherche en profondeur d'abord avec approfondissement itératif (``iterative deepening depth-first search'' en anglais) est une solution raisonnable comparée à la recherche en largeur, en ce qu'elle économise quantité de mémoire. Malheureusement, le temps nécessaire à prouver des formules croît en général exponentiellement en fonction de k et de la taille de la formule, de sorte que seuls de petits théorèmes faciles peuvent être prouvés à l'aide de cette stratégie.

Pour représenter l'incrémentation de k, nous ajoutons un étape d'extension à la procédure d'expansion de tableau : à tout moment dans la preuve, nous avons le choix d'ajouter une nouvelle instance Yr de Y au chemin courant, où r renomme toutes les variables libres de Y en de nouvelles variables. Nous pouvons alors faire appel à des heuristiques pour favoriser certaines étapes d'extension, dans l'espoir que nous pourrons ainsi clore le chemin plus vite qu'en se contentant les formules présentes dans le chemin courant. Le seul point à surveiller est l'équité du processus : nous ne devons pas appliquer les étapes d'extension en priorité indéfiniment longtemps, sinon la procédure deviendrait incomplète. Trouver les bonnes heuristiques est une tâche très compliquée, et c'est pourquoi nous ne nous y lancerons pas.