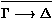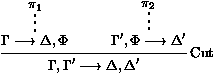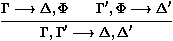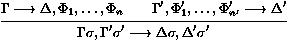La résolution comme preuve par coupure seulement

5 La résolution comme preuve par coupure seulement

Nous terminons ce chapitre par une analyse de ce que nous avons fait d'un point de vue de théorie de la preuve. Nous avons en effet développé la plus grande partie de la résolution, comme il est traditionnel, d'un point de vue essentiellement sémantique. Cependant, la règle de résolution ressemble tellement à la règle Cut de coupure dans le système de Gentzen LK qu'il doit exister une correspondance entre les deux (cf. ici dans le cas propositionnel). Cette correspondance, comme on peut s'y attendre, provient d'une variante du théorème d'élimination des coupures. Ceci apportera aussi une réponse à l'énigme : comme nous pouvons éliminer toutes les coupures, comment ceci justifie-t-il la résolution, où toutes les règles sauf la coupure sont éliminées ?

En premier, généralisons un peu le théorème d'élimination des coupures au premier ordre :

Théorème 31 [Élimination des coupures généralisée] Soit S un ensemble de séquents atomiques. Soit LK+S le calcul des séquents obtenu en ajoutant aux règles de LK toutes les règles de la forme :

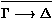
où G ¾® D est un séquent de S. De telles règles sont appelées des axiomes non logiques. Soit S_¥ le plus petit ensemble de séquents contenant S et stable par l'application de la règle Cut. (Autrement dit, si G ¾® D,F et F,G' ¾® D' sont dans S_¥, alors G, G' ¾® D, D' aussi.) Nous disons qu'une coupure est non logique si et seulement si ses prémisses sont toutes les deux dans S_¥. (Alors, sa conclusion est aussi dans S_¥.)

Alors un séquent atomique est prouvable dans LK+S si et seulement s'il est un affaiblissement d'un séquent prouvable dans LK+S par une preuve où toutes les coupures sont non logiques.
Preuve : Remarquons que les étapes d'affaiblissement peuvent être codées sous forme de coupures avec Ax, pourvu que le séquent affaibli ne soit pas vide. De plus, toute suite d'affaiblissements est équivalent à un affaiblissement unique : nous supposerons donc implicitement que la conclusion d'un séquent affaibli n'est jamais coupée avec Ax.

Nous montrons qu'un séquent est prouvable dans LK+S si et seulement s'il est dérivable par une preuve où les coupures sont soit non logiques, soit sont des coupures entre une version affaiblie d'un séquent de S_¥ et Ax (fournissant encore une version affaiblie du même séquent en conclusion).

La preuve est la même que pour le théorème d'élimination des coupures. Nous disons qu'une coupure est essentielle si elle est non logique et qu'elle n'est pas une coupure avec Ax. Nous allons éliminer toutes les coupures non essentielles.

Redéfinissons le rang de coupure r(p) d'une preuve p dans LK+S, comme valant 0 si p ne contient que des coupures essentielles (au lieu que p soit sans coupure dans le cas de LK), et sinon comme le maximum des d(p')+d(F), où p' parcourt toutes les sous-preuves de p se terminant sur une coupure logique entre deux preuves ne contenant que des coupures essentielles, et de formule de coupure F. Ensuite nous devons montrer que, pour toute preuve p de LK+S de rang de coupure non nul r, nous pouvons la transformer en une preuve de LK+S de rang au plus r-1 du même séquent, où aucune coupure non logique ne se trouve sous une coupure avec Ax.

Pour être sûr qu'aucune coupure non logique ne se trouve sous une coupure avec Ax, nous pouvons toujours pousser les coupures avec Ax (les affaiblissements) vers le bas de la dérivation : si G ¾® D produit G, G' ¾® D, D' par affaiblissement, et si nous inférons un séquent G'' ¾® D'' à partir de ce dernier par une règle R, alors soit R agit sur une formule qui était déjà dans GÈD, et les règles permutent, soit R agit sur une autre formule, et alors G'' ¾® D'' est une version affaiblie de G ¾® D, comme on peut le vérifier sur les règles de LK. Nous supposerons tacitement que cette normalisation est systématiquement effectuée.

Comme dans la preuve de l'élimination des coupures, choisissons une sous-preuve p' de p la plus haute possible (maximale) se terminant sur une coupure non essentielle sur F, avec d(p')+d(F) maximal. Alors p' est de la forme :

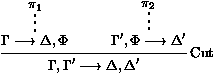
où p₁ et p₂ ne contiennent aucune coupure non essentielle. Comme nous avons supposé que tous les affaiblissements seraient systématiquement poussés en-dessous des autres coupures, p₁ et p₂ ne contiennent en fait aucune coupure logique (non essentielle ou affaiblissement).

Par construction, la dernière règle de p₁ n'est pas une coupure non logique, ou la dernière règle de p₂ n'est pas une coupure non logique. En effet, le contraire signifierait que la coupure ci-dessus est non logique, donc essentielle. Supposons sans perte de généralité que p₁ ne se termine pas sur une coupure non logique. Alors elle ne se termine pas par une coupure, parce que p₁ ne contient aucune coupure logique. Si p₂ ne se termine pas par une coupure, alors nous continuons comme dans le théorème d'élimination des coupures.

Sinon, p₂ se termine par une coupure non logique, et p₁ ne se termine pas par une coupure. Comme S_¥ ne contient que des séquents atomiques, la formule de coupure F doit être atomique. Alors, soit F n'est pas la formule principale dans la dernière règle de p₁, et nous faisons remonter la coupure le long de p₁; soit F est la formule principale, mais comme F est atomique, p₁ doit se terminer par une instance de Ax, de sorte que G,G' ¾® D,D' doit être un affaiblissement de G',F¾® D'; mais ceci contredit notre hypothèse que la coupure considérée était non essentielle.

Finalement, le processus termine comme avant, produisant une preuve où les seules coupures sont des coupures non logiques et des coupures avec Ax, et où les coupures avec Ax sont repoussées tout en bas de la preuve. Ces affaiblissements peuvent se résumer en au plus une coupure avec Ax, ce qui montre le théorème. ¤

Nous en déduisons la notion correspondante de propriété de sous-formule :

Corollaire 32 [Propriété de sous-formule étendue] Soit S un ensemble de séquents atomiques. Si G ¾® D est prouvable par une dérivation de LK+S où toutes les coupures sont non logiques, alors toutes les formules apparaissant dans la preuve sont des sous-formules de formules de G, D, ou apparaissent dans S.
Preuve : Par récurrence structurelle sur la preuve. Le seul point intéressant est quand nous arrivons sur la conclusion d'une règle de coupure non logique; mais alors toutes les formules, y compris la formule de coupure, apparaissent dans S_¥. Nous montrons que si elles apparaissent dans S_¥, alors elles apparaissent dans S. En effet, soit S₀ égale S, S₁ égale l'ensemble de toutes les conclusions de coupures sur des séquents de S₀, et en général soit S_n l'ensemble de niveau n; nous avons S_¥= È_nÎ_N S_n, et une récurrence facile sur n montre que l'ensemble des formules apparaissant dans S_n est exactement l'ensemble des formules apparaissant dans S. ¤

En particulier, si le séquent à déduire est le séquent vide, nous réobtenons la version de théorie de la preuve du théorème de complétude pour la résolution propositionnelle, d'une façon purement syntaxique :

Théorème 33 [Résolution] Soit F une formule propositionnelle en forme normale conjonctive. Considérons F comme un ensemble S de séquents atomiques. Alors F est incohérente si et seulement si le séquent vide ¾® est déductible de S et de la règle de coupure Cut uniquement.
Preuve : Par le théorème 31, si F est incohérente, alors nous pouvons dériver le séquent vide de S, en utilisant des coupures non logiques et les règles de LK autres que Cut, et en terminant éventuellement par une étape d'affaiblissement. Mais le seul séquent qui s'affaiblisse en le séquent vide est le séquent vide. Par le corollaire 32, cette preuve ne peut utiliser que des formules apparaissant dans S. Mais ceci implique qu'aucune autre règle que la coupure n'a pu être utilisée, d'où le résultat. ¤

Ensuite, pour relever ce résultat au cas des clauses du premier ordre, nous utilisons la version syntaxique du théorème de Herbrand et concluons qu'un ensemble de clauses S du premier ordre est incohérent si et seulement s'il existe un ensemble fini d'instances de ces clauses qui est incohérent.

L'unification est nécessaire parce que nous ne savons pas à l'avance de quelles instances nous aurons besoin. Autrement dit, nous remplaçons la règle de coupure habituelle :

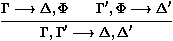
la règle suivante de ``coupure paresseuse'' :

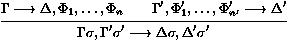
où n et n' sont non nuls, et F₁s = ... = F_ns = F'₁s' = ... = F'_n's'. Autrement dit, au lieu de produire toutes les instances des prémisses, et d'en trouver une sur laquelle nous pouvons appliquer la coupure, nous incluons le processus de calcul de ces instances dans la règle elle-même. Nous disons qu'il s'agit d'une règle ``paresseuse'' parce que nous ne sommes pas obligés de connaître toutes les liaisons de variables à des termes pour pouvoir l'utiliser.

Les considérations sur l'unification de la section 2 s'appliquent toujours, et nous pouvons encore coder cette règle comme la combinaison d'une règle de factorisation et d'une règle de résolution binaire.

La raison pour laquelle nous avons besoin de la factorisation, qui est une règle coûteuse en termes de non-déterminisme dans la recherche de la preuve, acquiert un nouveau sens : elle est l'expression de la règle implicite de contraction de la logique classique. En effet, lorsque nous appliquons la substitution s à un séquent, et si s unifie plusieurs formules dans le séquent, alors une étape automatique de contraction est effectuée, qu'il nous faut deviner par factorisation.

D'autres techniques ont aussi une justification en théorie de la preuve. Par exemple, l'effacement des tautologies revient à ignorer les instances de Ax : comme le théorème 31 le montre, nous ne pouvons pas ignorer Ax en général, puisque nous pourrions en avoir besoin lors d'une coupure à l'étape finale de la preuve d'un séquent G ¾® D de LK+S; mais si G et D sont vides, nous pouvons l'ignorer, parce que le seul séquent qui s'affaiblisse pour donner le séquent vide est le séquent vide lui-même. La raison pour laquelle l'élimination de tautologies fonctionne, alors, et que nous sommes capable de pousser toutes les coupures avec Ax en bas de la preuve, comme nous l'avons montré dans la preuve du théorème 31.

L'élimination des clauses subsumées est alors en partie justifiée par le même argument. Rappelons qu'une clause C=G ¾® D subsume C' si et seulement si C' est de la forme G', Gs ¾® Ds, D' pour une certaine substitution s, c'est-à-dire si C' est une version affaiblie d'une instance de C. L'affaiblissement n'est que la coupure avec Ax, et peut ainsi être poussée en bas de la preuve. Pour expliquer pourquoi les instances de clauses sont inutiles (sauf en tant que facteurs), nous devons recourir au lemme 12, que nous en fait déjà prouvé complètement syntaxiquement. (Autrement dit, contrairement au cas de la complétude de la résolution ordonnée, par exemple, nous n'avons pas eu à recourir à des considérations sémantiques, nous n'avons fait que déplacer des substitutions.)

Finalement, observons que les diverses stratégies, la résolution ordonnée, la résolution sémantique, la résolution linéaire, et ainsi de suite, sont des façons d'exprimer que la coupure sur une formule permute avec la coupure sur n'importe quelle autre formule, ce qui étend le théorème de permutabilité. Ces restrictions de la résolution peuvent alors être considérées comme des restrictions supplémentaires sur la forme des preuves du séquent vide n'utilisant que la coupure, dont le but est de les rendre plus canoniques. Cependant les preuves montrant que nous pouvons permuter les coupures sont compliquées par le fait que nous devons le faire modulo l'application de substitutions. C'est pourquoi les preuves de complétude de la résolution sémantique et de la stratégie ordonnée procédaient par raisonnement sur le cas pleinement instancié (non paresseux, ou clos), et relevaient ensuite le résultat au cas du premier ordre (paresseux).