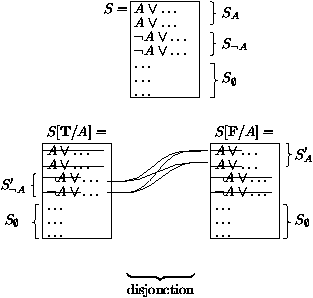
Figure 3: Séparation simulée par la résolution



| ¾® A,B |
| A¾® B |
| A,B¾® |
| B¾® A |
| ¾® P(a) |
| P(x) ¾® P(f(x)) |
| ¾® A,B |
| A¾® B |
| B¾® A |
| A,B¾® |
La raison pour laquelle cela fonctionne est le fait qu'au niveau propositionnel, la séparation sur A (l'atome maximal) consiste à calculer tous les résolvants de clauses sur A. Regarder la figure 3 : écrivons S comme l'union de trois ensembles : l'ensemble SA des clauses de la forme A Ú C, autrement dit les séquents avec A à droite; l'ensemble S¬ A des clauses de la forme ¬ A Ú C, autrement dit les séquents avec A à gauche; et l'ensemble SØ de toutes les clauses où A et ¬ A n'apparaissent pas. Nous supposons que les tautologies ont été éliminées, et donc ces trois ensembles sont disjoints. Soit S'A l'ensemble SA d'où A a été effacé, et de même pour S'¬ A et S¬ A.
Figure 3: Séparation simulée par la résolution
Les résolutions sémantiques guident les règles de résolution au moyen d'une interprétation I. Considérons la procédure de Davis-Putnam de nouveau. Dans le cas clos (propositionnel), la stratégie ordonnée revient à fixer un ordre sur les atomes clos A1, A2, ..., An; nous séparons alors sur A1, puis sur A2, et ainsi de suite. Les résolutions sémantiques contrôlent quelle branche nous explorons d'abord à chaque séparation. Chaque fois que nous souhaitons séparer sur Ai, nous pouvons essayer d'explorer le cas Ai vrai d'abord, puis le cas Ai faux; ou bien le contraire. Nous pouvons coder ce choix par une interprétation I : si I rend Ai vrai, alors nous choisissons d'explorer le cas Ai vrai d'abord, sinon nous explorons le cas Ai faux d'abord.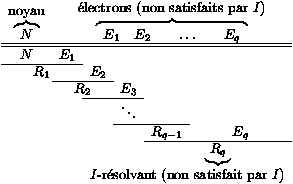
Figure 4: I-conflit en résolution sémantique
Le non-déterminisme est réduit, parce qu'un des clauses à résoudre est toujours fixée : c'est la dernière clause que nous avons produite par résolution. Le terme ``résolution linéaire'', qui ne se réfère pas à la logique linéaire, provient de la forme spéciale des dérivations par résolution dans ce cas : voir figure 5. Définissons :
Figure 5: Résolution linéaire
| CÙ A | ¬ A' Ù C' |
| (CÙ A)s | (¬ A' Ù C')s |


