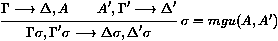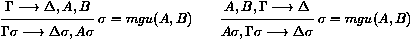Résolution

3 Résolution

Revenons à la règle de résolution. Rappelons que nous l'avons énoncée comme suit :

à partir des deux clauses C=G¾®D, A₁, ..., A_m et C'=A'₁, ..., A'_n, G'¾®D', déduire les clauses Gs, G's'¾® Ds, D's', pour toutes substitutions s et s' qui rendent égaux exactement A₁s, ..., A_ms à droite de C et A'₁s', ..., A'_ns' à gauche de C'.

Comme le mgu est unique, nous savons que toutes les clauses résultat Gs, G's'¾® Ds, D's' sont en fait des instances d'une clause unique : Gs, G'rs¾® Ds, D'rs, où r renomme les variables libres de la seconde clause en de nouvelles variables, non libres dans la première clause, et s est le mgu de A₁, ..., A_m, A'₁r, ..., A'_nr.

Ceci nous mène au principe de résolution, comme il est réellement utilisé en recherche de preuve par résolution :

Définition 8 [Résolution] La règle de résolution binaire est :

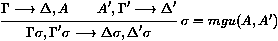
où nous supposons que les deux clauses G¾® D, A et A',G'¾®D' sont renommées de sorte qu'elles n'ont aucune variable libre en commun. La conclusion de la règle est appelée le résolvant binaire des deux clauses, les premisses sont appelées les clauses parentes, et A (resp. ¬ A') est le littéral sur lequel on résout dans la première clause (resp. second clause).

Nous disons que les littéraux A et ¬ A' sont complementaires à condition que A s'unifie avec A'.

La règle de factorisation est la règle double :

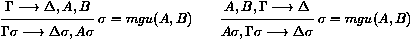
La conclusion de la règle est appelée un facteur binaire de la clause en prémisse.

Un facteur d'une clause est soit la clause elle-même, soit un facteur binaire d'un de ses facteurs. Un facteur propre d'une clause est un facteur d'un de ses facteurs binaires.

Un résolvant de deux clauses est un résolvant binaire de facteurs de chaque clause, non nécessairement propres.

Une dérivation par résolution est un arbre inversé dont les noeuds sont étiquetés par des clauses, les feuilles sont étiquetées par des clauses de l'ensemble initial de clauses, et les noeuds internes ont comme prédécesseurs leurs clauses parentes.

Une réfutation par résolution est une dérivation se terminant sur la clause vide, autrement dit une dérivation dont la racine est étiquetée par ¾®.

Remarquer que l'utilisation d'une règle séparée de factorisation code des unifications multiples.

Théorème 9 [Correction, complétude] Soit S₀ une ensemble de clauses, et S_n la suite des ensembles de clauses définie par S_n+1 égale l'ensemble de tous les résolvants de clauses dans S_n (S_n est appelé l'ensemble de niveau n).

Alors la résolution est une procédure de recherche de réfutation correcte et complète, autrement dit, l'ensemble S₀, vu comme une conjonction universellement quantifiée de clauses disjonctives, est insatisfiable si et seulement s'il existe nÎN tel que S_n, nÎN contienne la clause vide.
Preuve : La correction vient, comme dans le cas propositionnel, du fait que la conjonction de deux clauses quelconques (ici, universellement quantifiées) implique leurs résolvants.

La complétude est le fait que si S₀ est insatisfiable, alors il existe un ensemble de niveau qui contient la clause vide. Par les observations de la section 1, si S₀ est insatisfiable, alors l'ensemble des instances closes de clauses dans È_nÎ_NS_n contient la clause vide. (Ceci vient de la complétude de la résolution propositionnelle et du théorème de Herbrand.) Maintenant, la seule clause qui a la clause vide comme instance est la clause vide elle-même. Donc la clause vide est dans È_nÎ_NS_n, donc dans un des S_n. ¤

On peut avoir l'impression que la factorisation est inutile, et que les facteurs seront fabriqués par unification lors de la résolution binaire. Ceci simplifierait en effet le codage de la résolution. Malheureusement, les facteurs sont indispensables. Par exemple, l'ensemble des deux clauses :

¾® P(x,a), P(a,x)

P(y,a), P(a,y)¾®

est insatisfiable, parce que ¾® P(a,a) est une facteur de la première clause, P(a,a)¾® un facteur de la seconde, et la clause vide en est un résolvant. Cependant, les seules clauses que nous pouvons en extraire par résolution binaire uniquement sont P(a,x)¾® P(a,x), P(y,a)¾® P(y,a) et P(a,a)¾® P(a,a), mais pas la clause vide : la résolution binaire seule est incomplète.

Voir [CL73] pour une autre preuve de la complétude de la résolution. Chang et Lee procèdent par des arguments purement sémantiques, en utilisant des arbres de Herbrand, que nous avons déjà utilisés dans la preuve du théorème de Herbrand.