Unification

2 Unification

L'unification est le cas particulier où, étant donnés deux termes ou atomes s et t, nous voulons trouver l'ensemble des substitutions s telles que ss=ts. (À partir de maintenant, nous ne considérerons que le cas des termes, car les atomes ont la même structure que les termes.)

Définition 1  [Unificateur]   Soient s et t deux termes. Une substitution s est un unificateur de s et t si et seulement si ss = ts.

Ce cas particulier est suffisant pour résoudre notre problème. Nous le montrons en deux lemmes, mais d'abord une définition :

Définition 2  [Renommage]   Une substitution r est un renommage si et seulement si elle envoie des variables vers des variables, et elle est bijective.

Alors :

Lemme 3  [Unification avec renommage]   Soient s et t deux termes, et soit r un renommage envoyant les variables libres de t vers des variables non libres dans s.

Alors les couples (s,s') de substitutions tels que ss=ts' sont exactement les couples (s,rs), où s unifie s et tr.
Preuve : Exercice. ¤

Lemme 4  [Unification multiple]   Soient t₁, ..., t_n n termes, n³ 2. Il existe une substitution s telle que t₁s = ... = t_ns si et seulement s'il existe s₁ telle que t₁s₁ = t₂s₁, et s₂ telle que t₂s₁s₂ = t₃s₁s₂, et ..., et s_n-1 telle que t_n-1s₁ ... s_n-1= t_ns₁ ... s_n-1.
Preuve : Exercice. ¤

Pour trouver deux substitutions s et s' telles que A₁s= ...= A_ms= A'₁s'= ...= A'_ns', il suffit donc de renommer les A'_i's, 1£ i£ n, en A'_ir, où r envoie les variables de fv(A'₁)È ... È fv(A'_n) vers V\ (fv(A₁)È ... È fv(A_m)). Ensuite, par le lemme 3, il reste à unifier A₁, ..., A_m, A'₁r, ..., A'_nr. Par le lemme 4, nous pouvons le faire en unifiant les termes deux à deux, et en composant les substitutions au fur et à mesure.

Il reste à résoudre le problème de l'unification :

Étant donnés s et t, comment peut-on calculer l'ensemble des unificateurs de s et t?

Le résultat fondamental sur l'unification des termes du premier ordre est :

Théorème 5 [Unification] Soient s et t deux termes. Alors soit il n'existe aucun unificateur de s et t, et nous disons alors que s et t ne sont pas unifiables; ou il existe un unificateur le plus général ou mgu (``most general unifier'' en anglais), c'est-à-dire une substitution s telle que :

s est un unificateur de s et t, autrement dit, ss=ts;
et tout unificateur s' de s et t est une instance de s, c'est-à-dire qu'il existe une substitution s'' telle que s'=ss''.

Preuve : Omise (traité dans un autre cours du DEA). ¤

Le mgu, à strictement parler, peut ne pas être unique, car par exemple [x/y] et [y/x] sont toutes les deux des mgus des deux variables x et y. Mais on a une forme d'unicité à renommage près :

Lemme 6 [Unicité] Soient s et t deux termes. Alors les mgus de s et t sont unique à renommage près, c'est-à-dire que, pour tout couple de mgus s et s' de s et t, il existe un renommage r tel que s=s'r (et s'=sr^-1).

Nous notons mgu(s,t) le mgu (unique à renommage près) de s et t.
Preuve : Omise. ¤

Pour des raisons d'efficacité, nous représentons usuellement les unificateurs sous forme résolue comme :

Définition 7 [Forme triangulaire] Une forme triangulaire est une suite finie [t₁/x₁; t₂/x₂; ...; t_n/x_n] de liaisons terme/variable t_i/x_i. Nous disons qu'une forme triangulaire représente la substitution s si et seulement si s=[t₁/x₁] [t₂/x₂] ... [t_n/x_n]

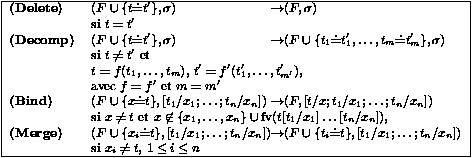
Figure 2: Règles d'unification

Voir la figure 2 pour un algorithme d'unification retournant une forme triangulaire, dans le style de Martelli et Montanari [MM82]. L'algorithme fonctionne en transformant des couples (F,s), où F est un ensemble ou un multi-ensemble de paires de termes (représentées comme des équations formelles non orientées entre termes) qui doivent être unifiées simultanément, et s est la forme triangulaire du mgu en cours de construction. En pratique, les multi-ensembles sont codés sous forme de listes, où l'ordre des éléments est jugé sans importance.

Pour commencer et unifier s et t, on lance l'algorithme sur ({s= t},[]). Ensuite, on choisit une règle à appliquer selon une stratégie donnée jusqu'à ce que plus aucune règle ne soit applicable. Une stratégie possible est la suivante : si F est vide, alors s est le mgu désiré; sinon, choisir une équation t= t' à résoudre dans F: si t égale t' (règle (Delete)), elle est déjà résolue, et on l'enlève simplement de F; si t et t' sont des applications du même symbole de fonction, alors seule la règle (Decomp) s'applique, et on remplace t= t' par les équations indiquées; si t ou t' est une variable, disons t, alors soit t n'est pas encore liée, c'est-à-dire qu'elle n'est pas dans le domaine de s, et on doit appliquer la règle (Bind) pour lier t à t'; ou elle est liée, et on doit remplacer l'équation t= t' par une nouvelle équation où t a été remplacée par sa valeur par la règle (Merge). Si aucune règle ne s'applique et F esta non vide, alors l'unification échoue.

L'algorithme qui en résulte prend toujours un temps polynomial en les tailles des termes de départ à unifier, et même un temps quasi-linéaire à condition de faire le test d'occurrence (xÏ{x₁,...,x_n}È fv(t[t₁/x₁] ... [t_n/x_n]); ``occurs-check'' en anglais) de la règle (Bind) de façon intelligente. Voir [JK90] pour un panorama sur l'unification, et plus.