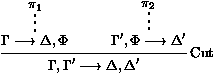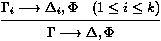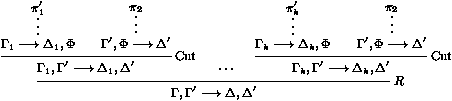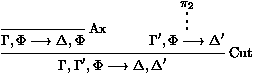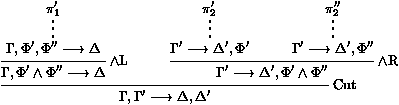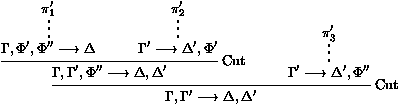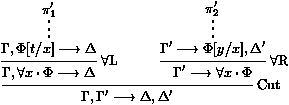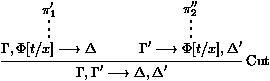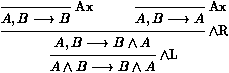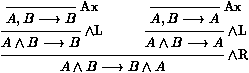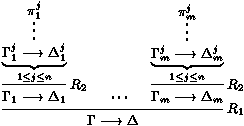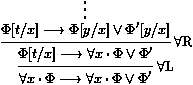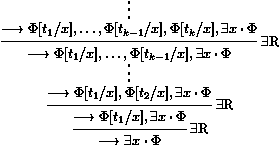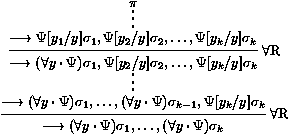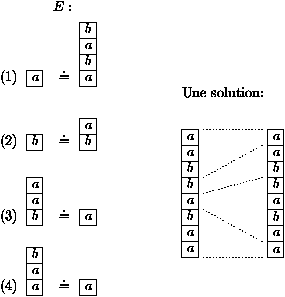
Figure 3: Un exemple du problème de correspondance de Post



Le problème de Post est indécidable; voir [DW85]. Nous pouvons de plus supposer que E ne contient pas l'équation (e, e), où e est le mot vide, et que l'alphabet ne contient que deux lettres distinctes a et b.
Figure 3: Un exemple du problème de correspondance de Post
| P(wj, w'j) Ù ¬ P(u |
|
(wj), v |
|
(w'j)) |
| P(a(vk), a(vk)) |
| P(b(vk), b(vk)) |
| P(e, e) | |||||||||
|
|||||||||
| ¬ P(a(vk), a(vk)) | |||||||||
| ¬ P(b(vk), b(vk)) |
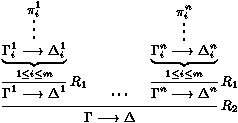
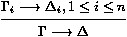 les séquents Gi¾®Di sont appelés les
prémisses, et G¾®D est la conclusion de la règle.
les séquents Gi¾®Di sont appelés les
prémisses, et G¾®D est la conclusion de la règle.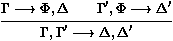 F est appelée la formule de coupure.
F est appelée la formule de coupure.